5月に更新された新型AIではもう十分にアーチェリー業務で実用的なレベルにあるという記事を書いてからは結構利用させていただいています。先日、歴史学で弓についての研究(?)というか研究の中で、矢の威力を扱っているものを読みましたが、計算がぜんぜん違うよな…となりまして、具体的には矢と銃弾を混同していて、銃弾は基本的にほぼ真っすぐ飛び、長距離になると下に落ちていきますが、矢は高さの到達点から落ちていきながら、位置エネルギーによって再加速されるのです。
質問をするために自分で矢の威力を計算したいとなりましたが、運動方程式が難しすぎるので、AIに任せてみました。AI(Copilot Pro)は自分では計算できないようです。よく考えれば、LLM(大規模言語モデル)ですので、計算はしないか。計算するためのコードは書いてくれるので、自分で計算することにしました。
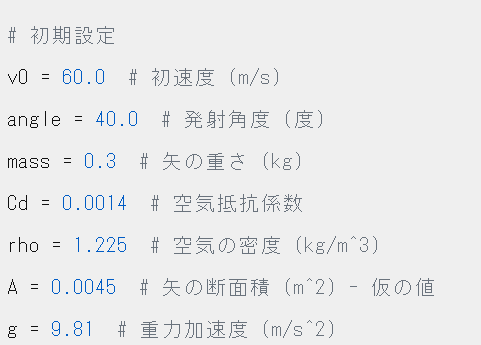
計算するに当たり、初期設定としては初速などが当然必要ですが、この数値の中で、空気抵抗係数だけがわからないのですが、ここも勉強してみたら難しそうだったので、調べたら直径7mm・20gのイーストンシャフトで測定した論文がありました。
こちらの論文では空気抵抗係数は1.94ということになっていましたのでこの数字を使って1、計算すると、一発で結果が出ました。
60m/sで40度で打ち出した場合、到達距離は237m、129m時点で最高高度に到達して59m。そこからは59mからものを落とすと加速するのと同じ理由で、最高点での33m/sから、的中までに7m/s(22%)、40m/sまで加速します。Copilotありがとう。考古学や歴史学で弓の威力について書かれる場合に、矢が再加速する性質を持っていることが無視される傾向にあると思います。
- H. O. Meyer, Applications of Physics to Archery, 2015 ↩︎
使用コード(Google Colab)
import math
import csv
# 初期設定
v0 = 60.0 # 初速度 (m/s)
angle = 40.0 # 発射角度 (度)
mass = 0.02 # 矢の重さ (kg)
Cd = 1.9 # 空気抵抗係数
rho = 1.225 # 空気の密度 (kg/m^3)
A = 0.000036 # 矢の断面積 (m^2)
g = 9.81 # 重力加速度 (m/s^2)
time_interval = 0.01 # 時間間隔 (s)
total_time = 10 # 計算する総時間 (s)
# 角度をラジアンに変換
angle_rad = math.radians(angle)
# 水平方向と垂直方向の初速度成分
v0x = v0 * math.cos(angle_rad)
v0y = v0 * math.sin(angle_rad)
# 速度と位置の初期値
vx = v0x
vy = v0y
x = 0
y = 0
# 結果を保存するリスト
trajectory_data = []
# 時間経過に伴う位置と速度の計算
for t in range(int(total_time / time_interval)):
# 空気抵抗力
Fd = 0.5 * Cd * rho * (vx**2 + vy**2) * A
# 空気抵抗による加速度
ax = -Fd / mass * (vx / math.sqrt(vx**2 + vy**2))
ay = -Fd / mass * (vy / math.sqrt(vx**2 + vy**2))
# 重力の影響を加えた垂直方向の加速度
ay -= g
# 速度の更新
vx += ax * time_interval
vy += ay * time_interval
# 位置の更新
x += vx * time_interval
y += vy * time_interval
# 現在の速度
velocity = math.sqrt(vx**2 + vy**2)
# 地面に達したら計算終了
if y <= 0:
break
# 結果をリストに追加
trajectory_data.append((t * time_interval, x, y, vx, vy, velocity))
# CSVファイルに保存
with open('trajectory_with_drag_and_velocity.csv', 'w', newline='') as file:
writer = csv.writer(file)
# ヘッダーを書き込む
writer.writerow(['Time (s)', 'X Position (m)', 'Y Position (m)', 'X Velocity (m/s)', 'Y Velocity (m/s)', 'Total Velocity (m/s)'])
# データを書き込む
writer.writerows(trajectory_data)
print('CSVファイルに軌道と速度のデータが保存されました。')The following two tabs change content below.
山口 諒
熱海フィールド代表、サイト管理人。日本スポーツ人類学会員、弓の歴史を研究中。リカーブ競技歴13年、コンパウンド競技歴5年、ベアボウ競技歴5年。リカーブとコンパウンドで全日本ターゲットに何度か出場、最高成績は準優勝。
最新記事 by 山口 諒 (全て見る)
- イーストン2025年、新商品はタングステンポイントです - 2024年12月3日
- Colt-Sahara National Open 1962 - 2024年12月2日
- 前方脱着ブリッジシステム BOSEN Ranger - 2024年12月1日
亀井さんのHPにある多分ヤマハが作成した資料の弾道曲線と結構違いますね。
https://www.a-rchery.com/arrow04.htm
ヤマハの技術者は正しい知識があると思うのでこのような資料は作らないと思います。
> その発射角 θ（°）、水平到達距離を Ｄ（ｍ）とすると、こんな式になります。前述の条件で９０ｍで１０点に的中させようとするなら、水平面から７°の角度で射ち出すことになります。
リンク見ましたが、60m/sの打ち出し角度7度で90m先の10点に当たるとしていますが、違います(重力加速度を9.81として)。
7度で射る場合、下の8点あたりに当たります(計算では高さ-15cmの場所に当たる)。
このサイトに関しては、根拠も算出時期もないのでこれ以上は想像です。
以前の記事で70年代のデータを2000年になっても正しいとしてアーチェリー教本に掲載されているけど、正しいわけないという記事を書きました。
https://archerreports.org/2021/08/%e6%ad%b4%e5%8f%b2%e3%81%aa%e3%82%93%e3%81%a6%e8%aa%bf%e3%81%b9%e3%81%a6%e4%bd%95%e3%81%97%e3%81%a6%e3%81%84%e3%82%8b%e3%81%ae%e3%81%8b/
画像を見るとイメージの解像度が著しく低いです。これも70年代のデータであると仮定すると、3:2というデータ算出はX7などで計算されていると考えられます。そこで70年代のワンピースボウ&1914のような大型シャフトと仮定して、矢の初速を遅くして、断面積を大きくして、矢を重くした結果、おおよそ、3:2の軌道をシミュレーションから得ることが出来ました。
私の見解としてはこのシミュレーションは50年前に行われたと推測します。当時の前提条件としては妥当かもしれませんが、今は2024年です。
コメントしたきっかけはこれを読んで思わず失笑してしまったからです。
> 具体的には矢と銃弾を混同していて、銃弾は基本的にほぼ真っすぐ飛び、長距離になると下に落ちていきますが、矢は高さの到達点から落ちていきながら、位置エネルギーによって再加速されるのです。
銃弾は矢よりも圧倒的に初速が早いので水平に発射しても見た目上直進して見えるだけで、上に向かって発射すれば高さの到達点から落ちてくるときに位置エネルギーを得られるし、矢だって水平に打てば位置エネルギーを得られずに失速するだけです。
最初はつりかな？と思ったのですが、どうやらマジでそう考えてるみたいですね。
> 矢の初速を遅くして、断面積を大きくして、矢を重くした結果、おおよそ、3:2の軌道をシミュレーションから得ることが出来ました。
リンク先の図では重力だけが作用する場合の定数として
距離＝90ｍ
初速＝毎秒60m
飛翔時間＝1.6秒
降下距離＝11.025ｍ
発射角＝7°
と書いてあるのに初速を変えてさらに距離＝35ｍ、降下距離＝3ｍで3:2になったとしてもそれはただの数字合わせで何の検証にもなってないですよ。
式にデータを代入して合わなかったのであれば合わなかったという結果で十分なのでは？
> 私の見解としてはこのシミュレーションは50年前に行われたと推測します。当時の前提条件としては妥当かもしれませんが、今は2024年です。
ちょっと調べてみたのですが、弾道学の歴史は古く18世紀までさかのぼるそうです。AIを使って調べるのは2024年だと思いますが、記事にある式はシンプルなのでそれなりに古いものじゃないですかね？最新というのであれば揚力・抗力、コリオリ力、マグナス効果のパラメータが欲しいですね。
>最初はつりかな？と思ったのですが、どうやらマジでそう考えてるみたいですね。
私もこちらのコメントは冗談かなと思ったのですが、長く書いていただいたので、マジで返信させていただきます。
大前提としてこれは現実の話です。ここを理解してください。夢の世界の話ではありません。
現実があって、シミュレーションに意味があります。
確かに理屈としてはおっしゃるとおりですが、”現実”において、銃弾はその直進性を利用した運用をされていて、矢はその弧を描く弾道を使用した運用がされています。
矢を大きな角度をつけて使用した記録は世界中に存在しますが、銃器を大きな角度をつけて運用した記録は少なくとも私は知りません。
初速が非常に高速な場合には着弾がある程度適切であれば良い砲弾にしか存在しない運用方法です。
現実に存在しない「銃弾の位置エネルギー利用」についてご意見を頂いても…でも、それ誰も使わないじゃん。としか言えません。
(追記) なぜ存在しないのか記事にしました。
https://archerreports.org/2024/06/bullets-from-the-sky/
(追記ここまで)
記事は読んでいただいてるようなので、まず、これは歴史についての話です。
宮本武蔵は五輪書で「弓の一徳は、はなつ矢、人の目に見へてよし。鉄炮の玉ハ、目にみヘざる所不足なり。」と書いています。
現代訳 弓の一つの長所は、放つ矢が人の目に見えて、（それが）よいのである。鉄砲の玉は目に見えないところがよくない。
(https://musasi.siritai.net/themusasi2/gorin/g104.htmlより)
弓の軌道、空から加速しながら落ちてくる視覚的効用については古くから語り継がれています。対して、銃弾も物理的には上から落ちてくるように飛ぶとしても、
宮本武蔵ほどの達人であっても見えないとしている以上、語る意味があるとは思いません。
(続く、後半は数字について検討します)
*銃弾の位置エネルギーによる事故は世界中で起きているので、無視できるとは思っていませんが、歴史上において戦闘に用いられたかという話をしています。
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14161131614
(前のコメントの続きです)
>リンク先の図では重力だけが作用する場合の定数として
>距離＝90ｍ
>初速＝毎秒60m
>飛翔時間＝1.6秒
>降下距離＝11.025ｍ
>発射角＝7°
繰り返しになりますが、↑という与えられた数字で、まず空気抵抗を考慮しない方法で計算しても、10点に当たりません。6時方向の8点になります。そちらの計算ではどういう結果ですか?
この時点でこのシミュレーションは正しくないと回答させていただきました。
>と書いてあるのに初速を変えてさらに距離＝35ｍ、降下距離＝3ｍで3:2になったとしてもそれはただの数字合わせで何の検証にもなってないですよ。
根拠も使用した式について私は公開していますが、リンク先のページでは何も示されていないので、そもそも検証のしようがありません。
検証してほしいのであれば、示してください。
その上で、3:2になる場合とかあるのかなと思って数字をいじってみて、
「ワンピースボウとX7ならそうなるかもね」
と回答させていただきましたが、このサイトに関しては、根拠も算出時期もないのでこれ以上は想像です。とお断りさせていただいたはずです。
私が「検証した」と言っていないものを「検証になっていない」とマジで言われても…想像だとお伝えしたはずです。
>ちょっと調べてみたのですが、弾道学の歴史は古く18世紀までさかのぼるそうです。AIを使って調べるのは2024年だと思いますが、記事にある式はシンプルなのでそれなりに古いものじゃないですかね？最新というのであれば揚力・抗力、コリオリ力、マグナス効果のパラメータが欲しいですね。
欲しいがっていることは伝わりましたが、他人に欲しがるばかりではなく、自分でも勉強してみたらどうですか? 私は今、学者の方と連絡を取って勉強させていただいていますが、相手が書かれたものについて間違っていると考えた場合には、その根拠や自分で再計算して、相手に対して指摘することが最低限の礼儀です。自分で汗もかかずに、「山口さん、私は匿名のものですが、亀井さんはあなたと違うこと書いていますよ」などという指摘はただの無礼です。
こんなことではあなたは「議論をする者」ではなく、ただの礼儀知らずになります。ご注意ください。
ニュートンの運動方程式はアインシュタインによって否定されました。それは20世紀前半のことです。しかし、今でも多くの人はニュートンの方程式を使います。”揚力・抗力、コリオリ力、マグナス効果のパラメータ”を使用することで結果がどれだけ変わるのかについては、どのような見識をお持ちですか?
最後にAIに聞いてみました。(1000km/時にしたのは私が今まで乗った一番速い乗り物が飛行機だからです。)
Q.時速1000kmの時、ニュートンの運動方程式とアインシュタインの運動方程式の結果はどれだけ違う?
A.時速1000km（約277.78m/s）では、ニュートンの運動方程式とアインシュタインの運動方程式の結果には顕著な違いはありません。
知恵袋ではこの差について計算した人がいるらしく、
“飛行機の速さを１００ｍ/ｓとして計算した場合、１秒につき、約３×１０＾－７秒遅れます。ちょうど１年間に１秒遅れるぐらいです。８０歳が寿命の人で２４時間８０年間飛行機に乗ったままだと、現実時間の８０秒だけ長く生きれます。”
だそうです。
*AIはCopilot Proを使用
**知恵袋 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1271369392
矢が落ちるときの再加速を戦国時代に用いていた記録がありましたので追記しておきます。関ヶ原から15年でそんな知識も失われてしまったのかと嘆く古老の話です。
*1熊沢淡庵 著 ほか『武将感状記』,人物往来社,1967. 国立国会図書館デジタルコレクション https://dl.ndl.go.jp/pid/2971280
*2 鈴木眞哉 著. 戦国合戦のリアル, PHP研究所, P366
一点指摘させていただきます。
ご承知だと思いますが、矢は発射時に与えられたエネルギーによってたわみを繰り返しながら飛翔する弾性体です。
ということは、空気抵抗に作用する進行方向に対する矢の投影面積はその断面積を最小として周期的に変化し、時間とともに変形によるエネルギー消費によってその振幅は減衰していくことになります。
ところがコラムでは断面積を定数として扱っているので、これは剛体を対象にしたものだと判断でき、掲載された結果は変形しない架空の矢のシミュレーションであると言えます。
ですから、「実際とは違いますが変形しない矢を使用した場合は」と注釈を入れるのが適切だと思います。
第一におっしゃる通りです。ご指摘ありがとうございます。
一番新しい記事で、ダーツでは下半身を使用しないと書きました。しかし、厳密にはそうではないと私も考えます。コメントいただいた記事は「頂点に達してから矢はどれだけ加速するか」という計算をしたものです。一方で、たわみは15m前後で収まります。そのために影響はほぽないと考えて記事を書いていますが、どの程度の影響があるとお考えでしょうか? 試算に対して20%の影響があるとしたら、再検討が必要だと私も考えます。10%未満であれば、無視してもよいのかなと現時点では考えています。
測定方法まだ把握していませんが、現在中継されているパリオリンピックで実際に計測されたデータを掲載しておきます。
山口さんはこのグラフをどう捉えていますか？
画面に定規を当てて計ってみたら発射位置を水平に伸ばした線とカーブが交わる点が約66MくらいになるのでMAX. HIGHTの33M辺りを中心に左右対称のグラフになっていて空気抵抗を加味してないみたいです。
弾頭の最高点(高さ)を測定するのに、例えば、35m時点での高さを最高とするという雑な運用はしていないと思いますが、+-2.5mか、+-5m程度の程度の測定結果を丸めて表示しているとかなと思っています。
追加、的にあたった瞬間に測定値が表示されているので、光学的な測定が行われているようです。この場合、静的測定は正確ですが、動的な測定は1/30フレームの場合で、3-5フレームを抽出して測定すると、誤差は220km/hの場合で約2-4mとなります。
この時は結構それっぽい数値が出てますが女子団体の韓国vsオランダのSOでは矢が10点のライン上にあるのに距離は70.3MM（CM表示は単なる単位間違いでしょう）と表示され9点判定になっていて結構誤差があってあまり信頼性は高くない感じです
あと、カメラのフレームレート30fpsで抽出に3-5フレーム必要というのは何か根拠はありますか？
今のモーションキャプチャー業界では240fpsが当たり前でオリンピックで民生品レベルの低性能なシステムを使うとはとても思えないんですけど
>今のモーションキャプチャー業界では240fpsが当たり前でオリンピックで民生品レベルの低性能なシステムを使うとはとても思えないんですけど
専門知識に基づいて240fpsのものが今回導入されている推測しているのであれば、そのとおりかもしれません。モーションキャプチャー業界について、自分はそれほどの知識がないのですが、コメント前半は今回のシステムは精度が低い、後半はシステムの性能が低いはずはないという、前半と後半で逆の主張のように読めるのですが、オリンピックの運営側は高い機械を使っているのに、単位も間違っているし、運用が下手で良い結果を出せていないというお考えの理解で正しいですか?
30fpsだと3-5フレームは必要というのは自分の経験則です。これはなにかの実験ではなく、防矢ネットの高さの計算のために撮った動画のときだった記憶があるので、もう少し賢いやり方があったのかもしれません。3-5フレームなければできない「はずだ」という意味ではなかったです。
> コメント前半は今回のシステムは精度が低い、後半はシステムの性能が低いはずはないという、前半と後半で逆の主張のように読めるのですが、オリンピックの運営側は高い機械を使っているのに、単位も間違っているし、運用が下手で良い結果を出せていないというお考えの理解で正しいですか?
言葉が足りなかったですね
システムと捉えてしまうと一塊に思ってしまうのは理解できますが実際にはソフトとハードに分かれていて僕らはそれらを組み合わせて使用してます
前半については「アプリの精度がいまいち」ってことですね
動画を見返してもらうと分かりますがこの「61.2MM」と表示された2秒後に「60.7MM」と表示が変わわります
画像認識プログラムによる計測結果は自動的に画面に表示されるようになっているはずですからこれはサンプリングもしくは判定基準が安定していない証拠で前に挙げたズレと合わせると使われているアプリは動作に難ありでもっと学習させて洗練させるべきだったというのが僕の見解です
後半についてはオリンピックの様なプロの現場で家電レベルの機材性能の話をしているのに違和感をもったので質問したわけですが自前の機材の話ならそれはまあそうだろうなあって感じですね
オリンピックの機材の話をすると2016年のリオから8K解像度の120fpsの超高精細でウルトラハイフレームレートなカメラが放送に導入されています
今回のグラフィカルな演出にもこのカメラの映像が使われていると僕は考えていていますがオンエアに使う機材だけで済まそうとしたため表現の一部に制約かかったのではないかとも考えています
例えば、混合団体の日本対トルコ戦のリリースポイントの表示では上下左右の差は表現してるのに前後の差はなくて同一ライン上にありました
このことからリリースポイントの位置データは選手を正面から撮影しているカメラの映像しか使用していない可能性が高いと考えています
同じ様に矢の軌跡のグラフも的の後ろの壁の上に設置されているカメラの映像から高さデータだけ取得してそれをゲームエンジンに食わせてそれっぽいカーブをリアルタイム生成してスパーインポーズしてるんじゃないかと想像してます
つまりグラフィカルな演出のために前後方向のデータの採取はやっていないというのが僕の予想です
オリンピックはエンターテインメントなのでそれっぽく見えれば番組的にはOKなので費用対効果を考えれば全てを正しくする必要はないです
正確ではない描写でも視聴者がそれに説得力を感じたらそれは演出的には大成功といったところじゃないかと思いますね
調べてみましたが、WAは2020年から採点システムにRyngDyng社のものを採用しているようです。下記システムの概要です。
https://www.archery-electronics.com/en/public/ryngdyng/technology
東京オリンピックのカメラシステムの概要は発表されていますが、パリオリンピックの概要はまだ出ていないかと思いますので、公式発表をまだ待つ段階ですかね。
https://docs.connect.panasonic.com/tokyo2020/proav/
>画像認識プログラムによる計測結果は自動的に画面に表示されるようになっているはずですからこれはサンプリングもしくは判定基準が安定していない証拠で前に挙げたズレと合わせると使われているアプリは動作に難ありでもっと学習させて洗練させるべきだったというのが僕の見解です
システムとしてはカメラ3台による三角測量システムを導入しているようです。複数の矢が的上にある状況下での測定が苦手なんですかね。次回に期待ということで!
>オリンピックの機材の話をすると2016年のリオから8K解像度の120fpsの超高精細でウルトラハイフレームレートなカメラが放送に導入されています
一点、導入されていることと使用されていることとは違うのかなと感じます。8k120fpsではデータ量が膨大になってしまって、競技・会場によっては使用に適さないのではないかと思います。オリンピックでは競技によっても大きく環境が違う(マラソンはスイッチングがメインだけど、アーチェリー競技はプレイバックが多い)ので、競技に合わせて、適切なレートを選択して放送している印象です。オリンピックアーチェリー競技に使用されているレベルの機材でも、ハイスピードカメラによって取得した動画が流れるまでに処理には結構な時間がかかっている印象です。
>このことからリリースポイントの位置データは選手を正面から撮影しているカメラの映像しか使用していない可能性が高いと考えています
はい、放送に使用されない測定に使用しているカメラはデータ量を削減するためにFHD程度の30fpsの非圧縮フォーマットでデータを取得しているのかなと思った次第です。
最後のあたりのゲームエンジンについては、全く触ったことがないのですが、アスリートが主人公であることを飛び越えない範囲で、これからもどんどん演出を取り入れていくのは良いのかなと思います。一方で、前回だったと思いますが、10%のアスリートが心拍数センサの装着を拒否しました。競技はアスリートファーストであることはいちばん大事であると思います。
> 一点、導入されていることと使用されていることとは違うのかなと感じます。8k120fpsではデータ量が膨大になってしまって、競技・会場によっては使用に適さないのではないかと思います。オリンピックでは競技によっても大きく環境が違う(マラソンはスイッチングがメインだけど、アーチェリー競技はプレイバックが多い)ので、競技に合わせて、適切なレートを選択して放送している印象です。オリンピックアーチェリー競技に使用されているレベルの機材でも、ハイスピードカメラによって取得した動画が流れるまでに処理には結構な時間がかかっている印象です。
一般の人がそう思い込むのは仕方がないですけどトリックのリプレイが多いスケートボードをNHKがBS8Kで放送してるしあのレベルのスローであればハイスピード素材でなくても編集機で十分対応可能だしそもそもメディアパートナーのパナソニックはハイスピードカメラをOBSに提供してないのでこれは事実誤認ですね
今回のオリンピックの映像技術的トピックとしてはフランスの公共放送が地上波で4KUHD放送してたりインテルの協力で8Kライブストリーミングをインターネットでしてるとかがあります
今は2024年なので色々と認識をアップデートした方がいいと思いますよ
コメントありがとうございます。話を整理させていただきたいと思いますが、技術は進化していくものですので、2023年の時点で、私の理解としては
・8K120fpsに対応できるカメラが導入されたとしてもすべてその情報量で撮影しているわけではない
・複数のフォーマットを組み合わせて中継している
・ハイスピードカメラは撮影してもそのまま使えず、編集できるデータにするのにデータの処理にある程度の時間がかかる
の3点の理解が認識が古いとご指摘の点だと理解しますが、どのような情報源を根拠としているのか教えていただけますか? アップデートさせていただきたいと思います。また、アーチェリー競技に話を限定させていください。(個人的にアーチェリー競技以外は100mとボルダリングも視聴しているので、これら競技の中継の話でも大丈夫ですが、引用されているスケートボードなどは見ていないのでわかりません)
>そもそもメディアパートナーのパナソニックはハイスピードカメラをOBSに提供してないのでこれは事実誤認ですね
前のコメントでも100mは見たと書きましたが、思い出したので、見返してみたら、決勝において、オメガが提供したハイスピードカメラによってゴール判定が行われています。パナソニックがハイスピードカメラを提供していないのかソースがないので判断しかねますが、正しいとしても、オメガが提供していればいい話ではないですか? 私としてハイスピードカメラはパナソニックと限定して話をすすめたことはないかと思いますので、事実誤認の論点が違うのかなと思います。
また、ゴール後、一刻も早く行われるべき勝者判定・ゴールシーンのリプレイにおいて、ハイスピードカメラで取得した映像が現場で放映されるまで、約3分かかっているので、編集作業自体にも時間がかかることは承知したうえで、ハイスピードカメラの動画が編集できるようになるまでには時間がかかるという私の理解は、2024年時点でも間違っていないと感じます。
山口さんの挙げた3つの理解自体は基本的に問題無いです
おかしいのはその認識から導き出した想像の部分でなんか変な思い込みがあるみたいですね
> 前のコメントでも100mは見たと書きましたが、思い出したので、見返してみたら、決勝において、オメガが提供したハイスピードカメラによってゴール判定が行われています。
これは確かにそうですねゴメンナサイ見落としてました
僕のコメントはこの部分に対する反応です
> オリンピックアーチェリー競技に使用されているレベルの機材でも、ハイスピードカメラによって取得した動画が流れるまでに処理には結構な時間がかかっている印象です。
少なくともアーチェリーの中継でやってたレベルのストレッチにハイスピードカメラを使うことはないです
ハイスピードカメラで検索して実機の仕様を見てもらうと分かると思いますがどれも録画時間が極端に短くて回し続けることは出来ないです
100Mのように収録のタイミングが確実に分かるもの以外でハイスピードカメラを使うのは無理があります
> オリンピックでは競技によっても大きく環境が違う(マラソンはスイッチングがメインだけど、アーチェリー競技はプレイバックが多い)ので、競技に合わせて、適切なレートを選択して放送している印象です。
全体の文脈からするとデータ量による負荷の問題が発生するので見せ方に合わせてフォーマットを変えてるってことですよね
東京から送出が4Kと8KになったのでパナソニックがOBSに提供しているシステムは4Kと8Kの両方に対応していて8Kを選択したときに機能制限があるという話は聞いたことがなくて競技によって変えなきゃいけない理由はないですね
あとNHKのBS8Kの番組表をみると日本で8K放送してるのは以下の競技です
バスケットボール・バレーボール・テニス・スケートボード・フェンシング・バスケットボール３×３・スケートボード・ブレイキン
正直これらの競技がなんで8K放送に選ばれたのか理由はよくわからないですがスイッチングがとかリプレイがとかは関係してないこことは確かだと思います
またこれはNHKの選択であってOBSがどの競技が4Kでどの競技が8Kで中継してるかの資料は見つからなかったので正確なことは言えないですがよその国ではたぶん別のラインナップなってるでしょうね
当然のことですが日本の地上波はリアルタイムに2Kにダウンコンして放送してます
> はい、放送に使用されない測定に使用しているカメラはデータ量を削減するためにFHD程度の30fpsの非圧縮フォーマットでデータを取得しているのかなと思った次第です。
たぶん圧縮すると書き込みに時間がかかると考えたんじゃないかと思うのですがハードウェアでデコードすればいいだけの話なのでデータが極端に大きくなる非圧縮はアプリに読み込むのに時間がかかるしメモリの消費も激しいので賢い選択ではないですね
> どのような情報源を根拠としているのか教えていただけますか? アップデートさせていただきたいと思います。
僕の言っていることは現場経験が入っているのでどこどこに書いてあるとか簡単に言えないですが普通の人がリーチできる情報源としてお勧めなのはPRONEWSですね
https://jp.pronews.com/
あと実機やオペレーションの様子が見たければInter BEEのに行ってみるのも面白いですよ
https://www.inter-bee.com/ja/
出始めは大砲みたいに大きかった放送用8Kカメラも最近は随分と小さくなりました
最後に全体的に感じたのは僕らと山口さんとではエンジニアリングに対するマインドがずいぶん違うなあということです
山口さんはデータの削減が絶対に必要と考えているようですが僕らはデータが大きくても安定してオンエアできるように対応して無用なリスクを避ける方向に動きますね
>ハイスピードカメラで検索して実機の仕様を見てもらうと分かると思いますがどれも録画時間が極端に短くて回し続けることは出来ないです
100Mのように収録のタイミングが確実に分かるもの以外でハイスピードカメラを使うのは無理があります
この前のコメントを受けて専門知識がある方と想定して返信していますが、おっしゃっていることが全く理解できません。失礼ですが、いつ頃のハイスピードカメラについての知識をお持ちですか?
私は4機種ほど扱ったことがあります。業務用機材としてはソニーのNEX-FS700を結構長い時間扱ってきました。下記の仕組みによって、1.5秒程度収録できれば、実用に耐えます。
ハイスピードカメラの収録時間が長くないことはおっしゃるとおりで、しかし、その原因は膨大なデータ量をバッファするメモリ量の限界であり、バッファメモリへ書き込みする事は、長時間可能です(あくまで秒単位に対する分単位という意味で”長”時間)。そのためドライブレコーダーの常時書き込みのように、メモリがいっぱいになったら古いデータに上書きすることで、長時間最新のデータを獲得することができます。
ハイスピードカメラの運用においては、この仕組を利用し、収録するイベントに対して、事前にトリガーを設定します。アーチェリーでFS700を使用する場合、ハーフトリガーに設定して、発射するタイミングで録画ボタンを押す事で、発射の週間の前後の4秒間のデータをバッファから記録媒体に収録することを行います。それがだいたい、アンカーに入ってから、的に当たるくらいまでのコンテンツになります。
コメントで情報源としたPRONEWSでも公開されている情報です。
「なお、ハイフレームレート撮影には、録画ボタンを押してから既定時間まで撮影するスタートトリガー、録画ボタンを押してから既定時間まで遡るエンドトリガー、遡る時間が半分に設定されたエンドトリガーハーフの3種類の記録開始方法から選択できる。」
https://jp.pronews.com/news/20150911163032908.html
トリガー方式をどのように設定できるのかは、そのカメラの性能に大きく関わることで、私が扱った事のある何百万のハイスピードカメラより、1桁値段の高いカメラは、トリガーを0.1usec単位で設定できます。
>僕の言っていることは現場経験が入っているのでどこどこに書いてあるとか簡単に言えないですが普通の人がリーチできる情報源としてお勧めなのはPRONEWSですね
ここまでの説明はすべて普通の人間がリーチできるレベルのネットの公開情報です。FS700のトリガー精度、バッファから記録媒体への書き込みにかかる時間など公開されていない情報があることはわかりますが、まずは公開されている情報レベルでのお話をしていただければ幸いです。
下記の回答はAIによって行われています。
>たぶん圧縮すると書き込みに時間がかかると考えたんじゃないかと思うのですがハードウェアでデコードすればいいだけの話なのでデータが極端に大きくなる非圧縮はアプリに読み込むのに時間がかかるしメモリの消費も激しいので賢い選択ではないですね
Q. スポーツなどの動画解析をするのに圧縮された高画質のものと無圧縮の低画質のものとどちらが最適ですか。データ量は同じとする。
スポーツなどの動画解析を行う場合、データ量が同じという条件下では、一般的に無圧縮の低画質の動画の方が最適と考えられます。その理由を以下に説明します:
## 無圧縮低画質動画の利点
1. **データの完全性**: 無圧縮動画は、元の映像データをそのまま保持しています。これにより、分析に必要な細かい情報が失われることなく保存されます[1]。
2. **フレームレートの維持**: 低画質であっても、無圧縮動画は通常高いフレームレートを維持できます。スポーツ分析では動きの連続性が重要なため、これは大きな利点となります[3]。
3. **編集の柔軟性**: 無圧縮データは後処理や編集の際により多くの選択肢を提供します。これは分析過程で重要になる可能性があります[5]。
## 圧縮高画質動画の課題
1. **情報の損失**: 高画質であっても、圧縮プロセスではある程度の情報が失われます。これは微細な動きや変化の分析に影響を与える可能性があります[1]。
2. **圧縮アーティファクト**: 圧縮動画には、ブロックノイズなどのアーティファクトが発生する可能性があります。これらは分析の精度に悪影響を及ぼす可能性があります[4]。
3. **フレーム間の予測**: 多くの圧縮技術は、フレーム間の予測を使用してデータ量を削減します。これにより、フレーム間の微細な変化が失われる可能性があります[6]。
## 結論
スポーツ動画解析では、動きの連続性、微細な変化、正確なタイミングなどが重要です。そのため、データ量が同じという条件下では、無圧縮の低画質動画の方が、圧縮による情報損失がなく、より正確な分析が可能になると考えられます。
ただし、実際の選択は具体的な分析目的や使用するソフトウェア、ハードウェアの性能などによっても変わる可能性があります。場合によっては、両方のタイプの動画を試して、より良い結果が得られる方を選択することも検討に値するでしょう。
Citations:
[1] https://safie.jp/article/post_14304/
[2] https://systemk-camera.jp/camera-blog/camera-system/compression-technology.php
[3] https://canon.jp/biz/trend/what-is-framerate
[4] https://www.stream.co.jp/blog/blogpost-13899/
[5] https://note.com/threeps/n/nd0c2ea4b1cf1
[6] https://qiita.com/daisukeoda/items/2f1badd24980c4fc3195
[7] https://info.securesamba.com/media/13138/
Q.私は収録して帰宅後にパソコンで確認するという方法でハイスピードカメラを運用していますが、中継システムにトリガー設定を導入できますか?
はい、放送中継のシステムにカメラのトリガー設定を導入することは可能です。実際に、多くの放送局やスポーツ中継で活用されています。
## トリガー設定の種類
カメラのトリガー設定には主に以下のようなものがあります:
– スタートトリガー: 撮影開始のタイミングを設定
– センタートリガー: 撮影中の特定のタイミングをマーク
– エンドトリガー: 撮影終了のタイミングを設定
## 導入のメリット
トリガー設定を導入することで以下のようなメリットがあります:
– 決定的瞬間の撮影漏れを防止
– 効率的な映像の切り出しや編集が可能
– ライブ中継とスロー再生の同時進行が容易に
## 具体的な活用例
スポーツ中継では、FT-ONE-LSなどの高速度カメラで多彩なトリガー入力が可能になっています[2]。これにより、撮影に応じた柔軟な設定ができ、必要な箇所だけを効率的に再生できるプリロール機能も備わっています。
また、ゴルフ中継などでは、ミリ波モバイルカメラシステムを使用し、トラブルショットの撮影に活用されています[3]。このシステムでは、高画質・低遅延でありながら、カメラのフルコントロールが可能です。
## 導入時の注意点
トリガー設定を導入する際は、以下の点に注意が必要です:
– カメラやスイッチャーなどの機器の互換性確認
– オペレーターのトレーニング
– 撮影シーンに応じた適切なトリガー設定の選択
## まとめ
カメラのトリガー設定は、放送中継の品質向上と効率化に大きく貢献する機能です。スポーツ中継や報道番組など、様々な場面で活用されており、今後もさらなる技術革新が期待されます。
Citations:
[1] https://www.nacinc.jp/analysis/high-speed-camera/memrecam-q5/
[2] https://www.eurecamera.com/case_study/sports.html
[3] https://www.nhk.or.jp/strl/publica/giken_dayori/97/5.html
[4] https://connect.panasonic.com/jp-ja/case-studies/marines
[5] https://www.ikegami.co.jp/case/
[6] https://www.sony.jp/camera-biz/casestudy/tvq/
[7] https://www.mediaedge.co.jp/product/23122
追記
>オリンピックの機材の話をすると2016年のリオから8K解像度の120fpsの超高精細でウルトラハイフレームレートなカメラが放送に導入されています
この返信を書くにあたって調べてみましたが、リオでNHKが使用したコーデックが120fps対応であることは確認しましたが、カメラは見つけられませんでした。情報源はございますか?
私が見つけた情報では「今回は4Kスーパースローモーションカメラで選手のプレーや技、表情を高速度撮影した映像を8K信号にU/C（Up Converter）してリプレイ再生した。」とあります。
リオデジャネイロオリンピックにおける NHKの8K SHV制作への取組み ITUジャーナル Vol. 46 No. 12（2016, 12）
滑らかな動きを表現する 高フレームレート映像符号化技術 NTTメディアインテリジェンス研究所
World’s first 8K TV broadcasts begin for Rio 2016 Olympics
> この前のコメントを受けて専門知識がある方と想定して返信していますが、おっしゃっていることが全く理解できません。失礼ですが、いつ頃のハイスピードカメラについての知識をお持ちですか?
そうですね不用意なコメントをしてしまいましたね
撤回します
ところで返事が無いですけど競技の内容によって4Kと8Kが使い分けられていないことやアーチェリーの放送でハイスピードカメラが使われていないのは確実だと思いますがこれについては同意してもらえますよね？
> 私は4機種ほど扱ったことがあります。業務用機材としてはソニーのNEX-FS700を結構長い時間扱ってきました。下記の仕組みによって、1.5秒程度収録できれば、実用に耐えます。
NEX-FS700は知らないカメラだったので調べましたが最大240fpsのカメラなんですね
これでやっと話がかみ合わない理由がわかりました
僕らがハイスピードカメラを使うのはだいたい秒1000～2000コマくらい必要なカットなのでそれ以下の性能のカメラは認識外でした
それに僕らが通常撮影に使うカメラでもスロー機能はついているので240fpsくらいだとハイスピードカメラとは思わないですね
あとアウトプットがMPEG-4 AVC/H264なのは画質的に放送素材としてはありえないのでそもそも選択肢に入らないです
業務用カメラなんでしょうけど音声さんやVEさんもいらない一人で撮って出しする結婚式場とかで使うレベルの機材っていう印象ですね
> Q. スポーツなどの動画解析をするのに圧縮された高画質のものと無圧縮の低画質のものとどちらが最適ですか。データ量は同じとする。
ゴメンナサイこれ何言ってるかわからないです
圧縮された高解像度と非圧縮の低解像度の間違いじゃないんですかね？
この問いだと解像度についての言及がないのでオリジナルに対して圧縮したけどなぜか高画質になっちゃったものと全く圧縮してないのでオリジナルと同じはずなのになぜか低画質になっちゃったものの両者のデータ量は同じって条件になってて支離滅裂なことを聞いてることこになってますよ！
僕がこういう質問をされてたら言ってることおかしくない？って即答しますね
> スポーツ動画解析では、動きの連続性、微細な変化、正確なタイミングなどが重要です。そのため、データ量が同じという条件下では、無圧縮の低画質動画の方が、圧縮による情報損失がなく、より正確な分析が可能になると考えられます。
山口さんの使ってるAIはこんな初歩的な間違いを指摘することなく無理やりストーリーを考えていかにもそれっぽい答えを生成してしまうですね
長々と考察の過程が書いてありますがAIが導き出したこの結論だと映像の解像度に関係なく高画質より低画質の方が良いってことになってるんですけどそれが正しいと思ってるんですか？
僕には高画質の動画と同じデータサイズの低画質の動画にどんなメリットがあるのか想像できないです
正直なところ色々と破綻してて話が通じないのも仕方ないなあって感じですね
> この返信を書くにあたって調べてみましたが、リオでNHKが使用したコーデックが120fps対応であることは確認しましたが、カメラは見つけられませんでした。情報源はございますか?
どうぞ
https://www.ituaj.jp/wp-content/uploads/2016/11/2016_12-01-Tokushu-NHK8K.pdf
せっかく書いていただきましたが、私のコメント読んでいますか? あなたの返信のレベルが低すぎます。
>NEX-FS700は知らないカメラだったので調べましたが最大240fpsのカメラなんですね
上の写真は前にも貼ったNEX-FS700のマニュアルですが、960fpsに対応しています。FS700とだけ入れてGoogle検索すると、ソニーストアのページが出ますが、すぐに仕様書にたどり着きます。
これが仕様書です。これに対しても、なにか(FHDの場合のデータを示したとか)言い訳か、謝罪をされるのでしょうが(私は実機を何年も使っているので960fpsなのは絶対に間違いない)、もうそれは結構なので、まず、あなたが正しく理解してからにしてください。FHDの場合は240fpsですが、前回の私の話の本質(ハイスピードカメラはトリガー設定で撮るのが常識)とは全く関係がありません。
>言葉が足りなかったですね
>そうですね不用意なコメントをしてしまいましたね 撤回します
>これは確かにそうですねゴメンナサイ見落としてました
と毎回自分のコメントのミスを認識いただいているのは良いことですが、こちらが提示したカメラの仕様書すら読めないか、読まないのか、わかりませんが、これでは議論になりません? 下記の私の前のコメントすら読んでいないですよね?
>どうぞ
>https://www.ituaj.jp/wp-content/uploads/2016/11/2016_12-01-Tokushu-NHK8K.pdf
これ、私が前のコメントで提示したリンク先なのですが、何を言いたいのかわかりません。もっとちゃんと読み込めという意味ですが? 前に「言葉足りず」と認めていますが、今回も言葉足らずとは思いませんか?
次回の返信でも同程度の、ググればわかるレベルの事実誤認があれば、もう返信するつもりはございません。疑問があったら自分で調べてください。
>ところで返事が無いですけど競技の内容によって4Kと8Kが使い分けられていないことやアーチェリーの放送でハイスピードカメラが使われていないのは確実だと思いますがこれについては同意してもらえますよね？
返信しているつもりですが、伝わっていないのなら、言い方を変えますが、私はアーチェリーしか見ていない(他にはボルダリングと100m)ので、他の競技について聞かれてもわかりません。
知らないです。
が返信になります。
(コメントを読んでいる他の方のために)
>これでやっと話がかみ合わない理由がわかりました
>僕らがハイスピードカメラを使うのはだいたい秒1000～2000コマくらい必要なカットなのでそれ以下の性能のカメラは認識外でした
>それに僕らが通常撮影に使うカメラでもスロー機能はついているので240fpsくらいだとハイスピードカメラとは思わないですね
無視しましたが、読んでいる方が勘違いしないために補足しておきます。このような考えはスポーツを扱うカメラ関係者の意見では全くありません。彼がそう思わないのは、個人の感想なので良いですが、業界全体の意見では決してありません。
日本の映像業界のトップとしてNHK放送技術研究所というものがあり、業界をリードする研究所の一つです。
そのNHK技研が240コマ(240fps)をハイスピードカメラとして分類しています。
一方で、ビデオサロンという玄光社が発行する日本で数少ない映像制作や動画編集に特化した月刊誌では、2012年7月号にて、私が議論の中で取り上げたFS700が表紙を飾り、FS700Jによるハイスピード撮影として特集も組まれていて、NHK技研のトップダウンだけではなく、ユーザー目線としてもハイスピード撮影であると認識されていることがわかります。
日本ではありませんが、米国映画テレビ技術者協会は250fps以上をハイスピードカメラと定義しています。
SMPTE（米国映画テレビ技術者協会）とは？| PRONEWS
自動車開発界隈のように240fpsでは何の意味もない業界も存在しますが、このサイトスポーツのアーチェリーを扱うものです。
以上、彼の主張は、彼が本当に映像業界の人間であれば、彼の感想以上のものではない、または、そもそも映像業界ではなく特殊な開発業務の従事者である可能性が高いことにご留意ください。
>山口さんはこのグラフをどう捉えていますか？
このコメントに対する返信です。WAの下記の投稿を見るとLiDARと機械学習を組み合わせて完全に軌道を取得しているようです。ご参考ください。
https://www.instagram.com/p/C-YJPDNqO97/
https://www.youtube.com/watch?v=ttYm4Qq7Mdk